(Continuation of part 1)
References
Everything I know about Nautilus Pompilius I learnt from these three knowledgeable sources:
[T] D'Arcy Wentworth Thompson, On growth and form (new edition, Cambridge University Press 1942)
[L] Neil H. Landman, Ontogeny of upper Cretaceous (Turonian-Santonian) scaphitid ammonites from the western interior of North America: systematics, developmental patterns, and life history. Bulletin of the American Museum of Natural History, volume 185 (1987), pp. 117-241.
[SL] W. Bruce Saunders and Neil H. Landman (editors), Nautilus, the biology and paleobiology of a living fossil (reprint with additions, Springer, 2009)
To verify our findings, or see for yourself (everything required will be at your disposal) you should download the marvelous free math tool Geogebra.
How I proceeded
1. I bought two halves of a Nautilus Pompilius shell (€ 11.95 a piece) at De Schelpenshop.
2. I put each half (in no particular position) on my CanoScan 9000F scanner, between two strips of graph paper on each of which I had marked by pin-holes the edges of two squares of 50 mm by 50 mm. These squares allow to detect and quantify any deformations caused by the scanning process. The raw results (TIFF files, 600 dpi) are here and here. I continued with the first one, because this one has more fine structure near the center.
3. Using Preview.app I transformed the tiff file into PNG, then pasted the image into a Geogebra worksheet, with the lower left corner at (0,0) and the lower right corner at (10,0). (Arbitrary choices, to attach the image to the axes while zooming and moving it.) I had Geogebra draw perfect squares on top of my scanned pin-holed squares, and found that the most distorted square (top right) had deviations of less than 0.5 mm in 50, i.e., less than 1%. Given the intrinsic imprecision (thickness of the Nautilus lines, possible and unknown inclination of the plane of the cut), I decided not to interfere with the scanned image. I then cropped the image to the sole shell (here) and pasted the cropped png image as pic1 into a new Geogebra sheet, with its lower left corner at (0,0) and its lower right corner at (10,0).
4. The axis of coiling (the pole of the logarithmic spiral) matters a lot, because we're dealing with an exponential, and a small imprecision results in a large deviation. In [T, p.758], several methods to locate the pole are described, to which [L, p.166] added a new one. Yet in [SL] two expert authors locate the pole differently (compare p.386, fig.11 to p.107, fig.1).
Fortunately, Geogebra allows a new high-precision technique to pinpoint the pole, which is as follows. Choose any two points A,B on the shell curve and have Geogebra display a vector with starting point X, bisecting the angle formed by XA and XB, and with the geometric mean of these radii as length. Move X around until the vector points exactly at a point, say C, of the shell curve. Then we have XA/XC=XC/XB, which is characteristic of the pole X.
If the shell curve were a geometric object and a perfect logarithmic spiral, this method would unambiguously lead from any two points A,B to the pole X. But the thickness of the walls of the nautilus allows some variation in choosing points "on the curve" and deciding when the vector points at a point "on the curve". Also, moving A and B along the shell may lead to different locations of the pole. So one should regard the pole, critical as it is, as a fuzzy spot subject to some manoeuvrability.
I had Geogebra compute the angle α by which the image should be rotated around X in order to give the left endpoint of the shell the ordinate of X. (This angle reflects how the shell happened to be placed on the scanner, and doesn't mean anything.)
I then defined a vector from X to the origin, translated pic1 by this vector (pic1' has the origin as pole), rotated pic1' (pic1'' shows the shell with its endpoint on the x-axis) and made pic1' invisible.
5. The equation r(t)=a exp(bt) implies that a=r(0) and that b can be determined from, e.g., r(4π)=a exp(4πb). I had Geogebra compute a,b from the points where the shell curve cuts the positive x-axis for the first time (Y, t=0) and for the third time (Z, t=4π). These points too are critical yet fuzzy.
In principle, the pole X and the points Y,Z define the logarithmic spiral unambiguously. In practice, I had to shuffle them around a bit before finding their optimal locations.
The findings
Here's a snapshot of my Geogebra screen. Right: pic1 (not entirely visible) with the points A,B,X, left: pic1'' with the points Y,Z and the logarithmic spiral (yellow) obtained after some shuffling with X,Y,Z.
Here the Construction Protocol:
Precision being what it is (or not), our particular measurement yields
a growth factor f2π very close to 3 (slightly larger),
a constant angle γ very close to 80° (slightly smaller).
One defines the other, of course, because the former is exp(2πb) and the latter arctan(1/b).
That the radius is tripled after each complete turn was observed as early as 1838! In that year, Henry Moseley read to the Royal Society his paper On the Geometrical Forms of Turbinated and Discoid Shells (here), which contains on p.356 the statement that it is a logarithmic spiral in which the distance of any two of its whorls measured upon a radius vector is one-third that of the two next whorls measured upon the same radius vector. The figure 6 on p.371 shows
with ab is one-third of bc. So if the distances to the pole are: of a=1, b=3 and c=9, then ab=2, being one third of bc=6.
The angle too, of some 80°, is generally accepted as typical of Nautilus Pompilius, other gastropods displaying larger angles, between 80° and 85°. [T, p.791]
Summarizing, the Nautilus Pompilius canon in round figures (Nautila Pompilia centerfold, so to speak) is:
Remarks.
1. Measurements in [SL, p.389] seem to reveal that the first few chambers (built in the embryonic phase) are somehow different from the overall pattern, but I found no reason to skip these, and could start the spiral at -π.
2. In [SL, p.427] the irregularity predicted for the body chamber is that the last 20-30° is less curved than the rest. Our findings for this particular shell, cut as it was, were different.
Nautilus, like the pyramids, is beloved by golden numberists because there are several impressive numbers, of dubious precision, to choose from. With some luck, you might strike gold, either φ=0.61803... or Φ=1.61803..., or some suitable power of one of these. In
Assuming that the right endpoint of the segment marked B is the pole (precision seems to have been deliberately avoided), the claim A/B=Φ is equivalent to
Unfortunately for the gullible among the American Entomologists, this claim is as blatantly wrong for the Nautilus as it is for the Parthenon: f2π is very close to 3, and nowhere near 2.61803... . But isn't fπ somewhere near 1.61803...? Or (which is actually the same thing) fπ/2 near √Φ? We leave you to explore these exciting possibilities.
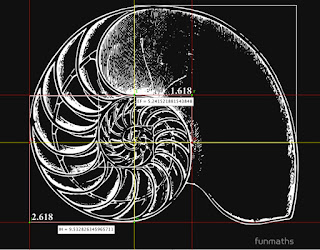
Update 2018-01-18. My wild guess that 'fπ might be somewhere near 1.61803...' has materialized in the T-shirt Fibonacci on a Nautilus shell by Funmaths. Fibonacci is nowhere involved, but the dogmatic statement fπ = Φ is proudly displayed: in half a turn, the radius increases from 1.618... (decimals not mentioned) to 2.618... (decimals not mentioned).
I used Geogebra (see below) to measure the distances given by Funmaths for their T-shirt pet, and found a growth factor IH/EF = 1.818..., nowhere near 1.618... In a real nautilus (like the one above that I measured) f2π is very close to 3, hence fπ very close to the square root, which is 1.732... Sadly, Golden Dream Dogmas made it into the very math promoting business.
Here is what this funmath should look like:
Summarizing, the Nautilus Pompilius canon in round figures (Nautila Pompilia centerfold, so to speak) is:
Remarks.
1. Measurements in [SL, p.389] seem to reveal that the first few chambers (built in the embryonic phase) are somehow different from the overall pattern, but I found no reason to skip these, and could start the spiral at -π.
2. In [SL, p.427] the irregularity predicted for the body chamber is that the last 20-30° is less curved than the rest. Our findings for this particular shell, cut as it was, were different.
Golden dreams
Nautilus, like the pyramids, is beloved by golden numberists because there are several impressive numbers, of dubious precision, to choose from. With some luck, you might strike gold, either φ=0.61803... or Φ=1.61803..., or some suitable power of one of these. In
Matthew S. Lehnert e.a., The Golden Ratio reveals geometric differences in Proboscis coiling among butterflies of different feeding habits, American Entomologist 61 (2015), pp.18-26 (here)we find, closely following the Parthenon (p.18), this artist's impression and caption (p.19):
 |
| the Golden Ratio, shown here in the shell of a nautilus, holds that the ratio of two parts (A and B here) is equal to the ratio of the larger of the two (A) to the whole (C, which equals A+B). |
Assuming that the right endpoint of the segment marked B is the pole (precision seems to have been deliberately avoided), the claim A/B=Φ is equivalent to
f2π=1+Φ.
Update 2018-01-18. My wild guess that 'fπ might be somewhere near 1.61803...' has materialized in the T-shirt Fibonacci on a Nautilus shell by Funmaths. Fibonacci is nowhere involved, but the dogmatic statement fπ = Φ is proudly displayed: in half a turn, the radius increases from 1.618... (decimals not mentioned) to 2.618... (decimals not mentioned).
I used Geogebra (see below) to measure the distances given by Funmaths for their T-shirt pet, and found a growth factor IH/EF = 1.818..., nowhere near 1.618... In a real nautilus (like the one above that I measured) f2π is very close to 3, hence fπ very close to the square root, which is 1.732... Sadly, Golden Dream Dogmas made it into the very math promoting business.
*